La logique formelle et le raisonnement par récurrence sont des concepts fondamentaux en mathématiques, qui s’imbriquent parfaitement pour assurer la validité des démonstrations. Une bonne appréhension de ces notions permet notamment de développer une pensée critique et rigoureuse, essentielles dans des domaines variés allant de l’arithmétique à l’informatique. Cet article propose d’explorer en profondeur les principes sous-jacents à ces concepts, leur interaction, et leur application dans le cadre de preuves formelles.

Définition de la logique formelle
La logique formelle est une discipline qui s’intéresse à la structure des arguments. Elle fournit un cadre permettant de déterminer si une proposition est vraie ou fausse en fonction des règles bien définies. Ces règles permettent d’analyser des énoncés sous diverses formes : propositions logiques, quantificateurs, connecteurs logiques, et axiomes.
Les propositions et leur valeurs de vérité
La base de la logique formelle repose sur les propositions, qui sont des énoncés pouvant être classés comme vraies ou fausses. Par exemple, une proposition telle que « 2 + 2 = 4 » est vraie, tandis que « 2 + 2 = 5 » est fausse. L’étude des propositions se prolonge en examinant les relations entre elles.
Les connecteurs logiques jouent un rôle crucial, formant des énoncés plus complexes à partir de propositions simples. Les principaux connecteurs incluent :
- ET (conjonction)
- OU (disjonction)
- NON (négation)
- IMPLIQUE (implication)
- ÉQUIVALENT (équivalence)
Ces connecteurs permettent de construire des systèmes d’énoncés logiques qui engendrent des conclusions. Par exemple, dans un système formel, l’énoncé « Si P alors Q » souligne que la vérité de P entraîne celle de Q, ce qui mène à des inférences essentielles dans le raisonnement formel.
| Connecteur | Exemple | Valeur de vérité |
|---|---|---|
| ET | P : « Il pleut » Q : « Il fait froid » P ET Q : « Il pleut et il fait froid » |
Vrai si P et Q sont vraies |
| OU | P : « Il pleut » Q : « Il fait froid » P OU Q : « Il pleut ou il fait froid » |
Vrai si au moins l’un est vrai |
| NON | P : « Il pleut » NON P : « Il ne pleut pas » |
Inverse la valeur de vérité |
Le raisonnement par récurrence : principes fondamentaux
Le raisonnement par récurrence, ou induction mathématique, est un outil puissant pour prouver des propriétés qui s’appliquent à tous les entiers naturels. Ce type de raisonnement repose sur un principe simple, similaire à celui d’un escalier : si l’on peut prouver qu’une propriété est vraie pour une première marche et qu’on peut démontrer qu’elle reste vraie d’une marche à l’autre, alors elle est vraie pour toutes les marches suivantes.
Les étapes du raisonnement par récurrence
Le raisonnement par récurrence se déroule typiquement en trois étapes :
- Initialisation : Vérifiez que la propriété est vraie pour le cas de base, généralement (n = 0) ou (n = 1).
- Hérédité : Supposez que la propriété est vraie pour un entier (n) et montrez qu’elle doit donc être vraie pour (n + 1).
- Conclusion : Dans ce cas, la propriété est alors valide pour tous les entiers naturels.
Examinons cette méthode à travers un exemple classique : la somme des n premiers entiers naturels, donnée par la formule :
[S(n) = 1 + 2 + ldots + n = frac{n(n+1)}{2}.]
Initialisation : Pour (n = 1), (S(1) = 1 = frac{1(1+1)}{2}), ce qui est vrai.
Hérédité : Supposons que cela est vrai pour (n), c’est-à-dire que (S(n) = frac{n(n+1)}{2}). Alors pour (n + 1) :
[S(n+1) = S(n) + (n + 1) = frac{n(n+1)}{2} + (n + 1) = frac{n(n+1) + 2(n + 1)}{2} = frac{(n + 1)(n + 2)}{2}.]
Conclusion : La propriété est donc maintenue pour tous les n entiers naturels.
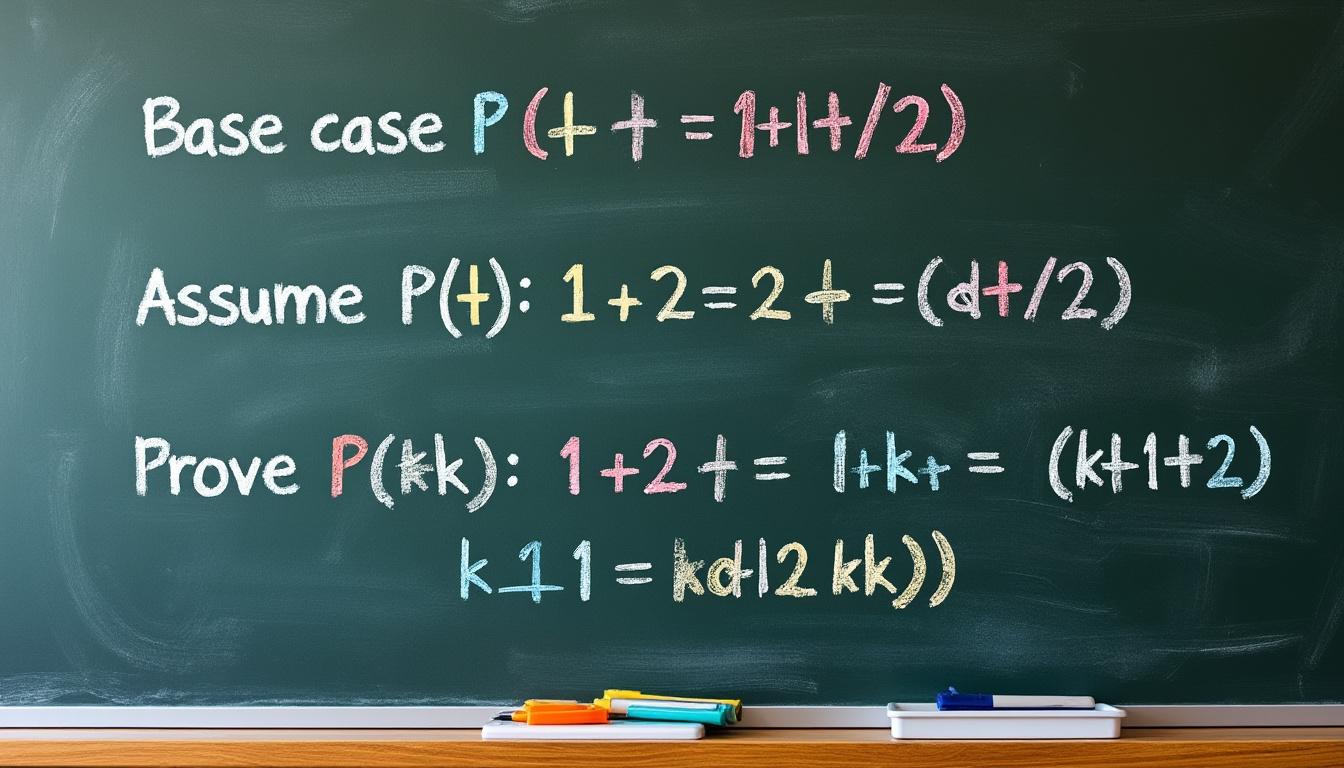
Applications pratiques et théoriques du raisonnement par récurrence
Le raisonnement par récurrence trouve des applications dans de nombreux domaines, y compris l’arithmétique, l’informatique, et d’autres champs scientifiques. Il est essentiel pour démontrer des théorèmes, prouver les propriétés des suites, des séries et établir des algorithmes.
Exemples d’applications
Voici quelques domaines où le raisonnement par récurrence est utilisé :
- Théorèmes en théorie des nombres : Preuves sur la divisibilité, comme démontrer que pour tout entier n, (n^2) est impair si n est impair.
- Analyse algorithmique : Dans le cadre de l’analyse des performances d’algorithmes comme ceux de tri, où le temps d’exécution peut souvent être décrit par une relation de récurrence.
- Graphes et combinatoire : Preuves de motifs dans les graphes et les structures combinatoires.
| Domaine | Application | Exemple de propriété prouvée |
|---|---|---|
| Théorie des nombres | Démonstration d’identités arithmétiques | Pour tout n, n^2 + n est pair |
| Informatique | Analyse de la complexité d’algorithmes | Démonstration par récurrence d’un algorithme de tri |
| Combinatoire | Propriétés des variantes de graphes | Le nombre de chemins entre deux nœuds |
Le lien entre logique formelle et raisonnement par récurrence
Il devient évident que la logique formelle et le raisonnement par récurrence sont étroitement liés. Le raisonnement par récurrence utilise les fondements établis par la logique formelle pour construire des démonstrations rigoureuses. Chaque étape du raisonnement s’appuie sur des énoncés clairs et précis, ce qui garantit que la conclusion soit valide et que les erreurs soient minimisées.
Importance de la rigueur dans les démonstrations
La rigueur est primordiale dans les preuves formelles en mathématiques. Les petites erreurs dans la logique peuvent mener à des conclusions fausses. Utiliser des systèmes formels et respecter les règles de la logique permet de minimiser ces risques. Voici quelques conseils pratiques pour assurer la clarté des démonstrations :
- Utiliser des définitions claires : Chaque terme doit être clairement défini au début de la démonstration.
- Suivre un raisonnement logique : S’assurer que chaque étape découle logiquement de la précédente.
- Rédiger explicativement : Rendre explicites toutes les étapes et conclusions pour que le raisonnement soit compréhensible par tous.
Conclusion et perspectives
En somme, la logique formelle et le raisonnement par récurrence offrent un cadre puissant pour comprendre et démontrer des propriétés mathématiques. Leur interconnexion permet d’établir des vérités mathématiques d’une manière rigoureuse et systématique, ce qui est essentiel pour toute personne cherchant à approfondir ses connaissances en mathématiques. Ces concepts représentant des outils indispensables dans le répertoire des mathématiciens, leur maîtrise ouvre des portes vers des domaines variés tels que l’informatique théorique, la cryptographie ou même les sciences sociales, où une pensée rigoureuse est cruciale.
Qu’est-ce que la logique formelle ?
La logique formelle est une branche des mathématiques qui étudie les règles et principes permettant d’analyser la validité des arguments et des propositions.
Comment prouver par récurrence ?
Pour prouver par récurrence, il faut démontrer la validité pour le cas de base, puis prouver que la validité du cas n’implique celle du cas n+1.
Pourquoi le raisonnement par récurrence est-il utilisé ?
Le raisonnement par récurrence est utilisé pour prouver des propriétés qui s’appliquent aux entiers naturels, notamment dans les théorèmes de combinatoire, d’arithmétique et d’algorithmique.
Quelle est la différence entre un axiome et une proposition ?
Un axiome est une affirmation acceptée sans preuve dans un système formel alors qu’une proposition nécessite une démonstration pour établir sa véracité.
En quoi la logique formelle est-elle importante ?
La logique formelle est essentielle dans les mathématiques car elle fournit un cadre rigoureux pour analyser et prouver des propos, minimisant ainsi les erreurs dans le raisonnement.




